George Pólya
Appearance
(Redirected from George Polya)

George Pólya (December 13, 1887 – September 7, 1985) was a Hungarian mathematician and professor of mathematics at ETH Zürich and at Stanford University. His work on heuristics and pedagogy has had substantial and lasting influence on mathematical education, and has also been influential in artificial intelligence.
Quotes
[edit]- "Groping" and "muddling through" is usually described as a solution by trial and error. ...a series of trials, each of which attempts to correct the error committed by the preceding and, on the whole, the errors diminished as we proceed and the successive trials come closer and closer to the desired final result. ...we may wish a better characterization ..."successive trials" or "successive corrections" or "successive approximations." ...You use successive approximations when ...looking for a word in the dictionary ...A mathematician may apply the term ...to a highly sophisticated procedure ...to treat some very advanced problem ...that he cannot treat otherwise. The term even applies to science as a whole; the scientific theories which succeed each other, each claiming a better explanation ...may appear as successive approximations to the truth.
Therefore, the teacher should not discourage his students from using trial and error—on the contrary, he should encourage the intelligent use of the fundamental method of successive approximations. Yet he should convincingly show that for ...many ... situations, straightforward algebra is more efficient than successive approximations.- George Pólya, Mathematical Discovery: On Understanding, Learning, and Teaching Problem Solving (1962)
- Mathematics is the cheapest science. Unlike physics or chemistry, it does not require any expensive equipment. All one needs for mathematics is a pencil and paper.
- Jon Fripp; Michael Fripp; Deborah Fripp (2000). Speaking of Science: Notable Quotes on Science, Engineering, and the Environment. Newnes. p. 45. ISBN 978-1-878707-51-2.
How to Solve It (1945)
[edit]- Unless otherwise stated, page references are from the Expanded Princeton Science Library Edition (2004) ISBN 0-691-11966-X
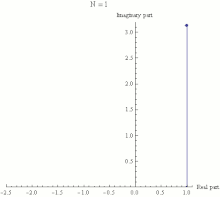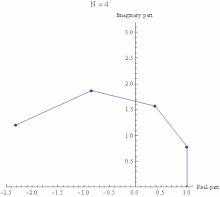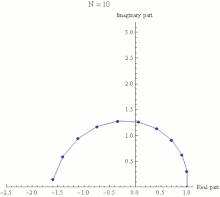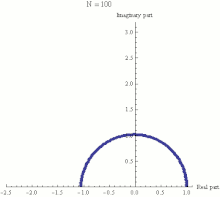
- There was a seminar for advanced students in Zürich that I was teaching and von Neumann was in the class. I came to a certain theorem, and I said it is not proved and it may be difficult. Von Neumann didn't say anything but after five minutes he raised his hand. When I called on him he went to the blackboard and proceeded to write down the proof. After that I was afraid of von Neumann.
- 2nd ed. (1957), p. xv
- Analogy pervades all our thinking, our everyday speech and our trivial conclusions as well as artistic ways of expression and the highest scientific achievements.
- p. 37
- Euclid's manner of exposition, progressing relentlessly from the data to the unknown and from the hypothesis to the conclusion, is perfect for checking the argument in detail but far from being perfect for making understandable the main line of the argument.
- p. 70
- The best of ideas is hurt by uncritical acceptance and thrives on critical examination.
- p. 100
- We need heuristic reasoning when we construct a strict proof as we need scaffolding when we erect a building.
- p. 113
- Pedantry and mastery are opposite attitudes toward rules. To apply a rule to the letter, rigidly, unquestioningly, in cases where it fits and in cases where it does not fit, is pedantry. … To apply a rule with natural ease, with judgment, noticing the cases where it fits, and without ever letting the words of the rule obscure the purpose of the action or the opportunities of the situation, is mastery.
- p. 148
- To write and speak correctly is certainly necessary; but it is not sufficient. A derivation correctly presented in the book or on the blackboard may be inaccessible and uninstructive, if the purpose of the successive steps is incomprehensible, if the reader or listener cannot understand how it was humanly possible to find such an argument....
- p. 207
- The cookbook gives a detailed description of ingredients and procedures but no proofs for its prescriptions or reasons for its recipes; the proof of the pudding is in the eating. … Mathematics cannot be tested in exactly the same manner as a pudding; if all sorts of reasoning are debarred, a course of calculus may easily become an incoherent inventory of indigestible information.
- p. 219
Induction and Analogy in Mathematics (1954)
[edit]Vol. 1. Of Mathematics and Plausible Reasoning
- Demonstrative reasoning penetrates the sciences just as far as mathematics does, but it is in itself (as mathematics is in itself) incapable of yielding essentially new knowledge about the world around us. Anything new that we learn about the world involves plausible reasoning, which is the only kind of reasoning for which we care in everyday affairs.
- Everyone knows that mathematics offers an excellent opportunity to learn demonstrative reasoning, but I contend also that there is no other subject in the usual curricula of the schools that affords a comparable opportunity to learn plausible reasoning. ...let us learn proving, but also let us learn guessing.
- The result of the mathematician's creative work is demonstrative reasoning, a proof; but the proof is discovered by plausible reasoning, by guessing. If the learning of mathematics reflects to any degree the invention of mathematics, it must have a place for guessing, for plausible inference.
- In plausible reasoning the principal thing is to distinguish... a more reasonable guess from a less reasonable guess.
- The general or amateur student should also get a taste of demonstrative reasoning... he should acquire a standard with which he can compare alleged evidence of all sorts aimed at him in modern life.
- The efficient use of plausible reasoning is a practical skill and it is learned... by imitation and practice. ...what I can offer are only examples for imitation and opportunity for practice.
- I shall often discuss mathematical discoveries... I shall try to make up a likely story how the discovery could have happened. I shall try to emphasize the motives underlying the discovery, the plausible inferences that led to it... everything that deserves imitation.
- I... present also examples of historic interest, examples of real mathematical beauty, and examples illustrating the parallelism of the procedures in other sciences, or in everyday life.
- For many of the stories told the final form resulted from a sort of informal psychological experiment. I discussed the subject with several different classes... Several passages... have been suggested by answers of my students, or... modified... by the reaction of my audience.
Mathematical Methods in Science (1977)
[edit]- In my presentation I... follow the genetic method. The essential idea... is that the order in which knowledge has been acquired by the human race will be a good teacher for its acquisition by the individual. The sciences came in a certain order; an order determined by human interest and inherent difficulty. Mathematics and astronomy were the first sciences really worth the name; later came mechanics, optics, and so on. At each stage of its development the human race has had a certain climate of opinion, a way of looking, conceptually, at the world. The next glimmer of fresh understanding had to grow out of what was already understood. The next move forward, halting shuffle, faltering step, or stride with some confidence, was developed upon how well the [human] race could then walk. As for the human race, so for the human child. But this is not to say that to teach science we must repeat the thousand and one errors of the past, each ill-directed shuffle. It is to say that the sequence in which the major strides forward were made is a good sequence in which to teach them. The genetic method is a guide to, not a substitute for, judgement.
- Introduction
- Why should the typical student be interested in those wretched triangles? ...He is to be brought to see that without the knowledge of triangles there is not trigonometry; that without trigonometry we put back the clock millennia to Standard Darkness Time and antedate the Greeks.
- Good approximations often lead to better ones.
- The volume of the cone was discovered by Democritus... He did not prove it, he guessed it... not a blind guess, rather it was reasoned conjecture. As Archimedes has remarked, great credit is due to Democritus for his conjecture since this made proof much easier. Eudoxes... a pupil of Plato, subsequently gave a rigorous proof. Surely the labor or writing limited his manuscript to a few copies; none has survived. In those days editions did not run to thousands or hundreds of thousands of copies as modern books—especially, bad books—do. However, the substance of what he wrote is nevertheless available to us. ...Euclid's great achievement was the systematization of the works of his predecessors. The Elements preserve several of Eudoxes' proofs.
- Mathematics succeeds in dealing with tangible reality by being conceptual. We cannot cope with the full physical complexity; we must idealize.
- We wish to see... the typical attitude of the scientist who uses mathematics to understand the world around us. ...In the solution of a problem ...there are typically three phases. The first phase is entirely or almost entirely a matter of physics; the third, a matter of mathematics; and the intermediate phase, a transition from physics to mathematics. The first phase is the formulation of the physical hypothesis or conjecture; the second, its translation into equations; the third, the solution of the equations. Each phase calls for a different kind of work and demands a different attitude.
- Facing any part of the observable reality, we are never in possession of complete knowledge, nor in a state of complete ignorance, although usually much closer to the latter state.
- If we deal with our problem not knowing, or pretending not to know the general theory encompassing the concrete case before us, if we tackle the problem "with bare hands", we have a better chance to understand the scientist's attitude in general, and especially the task of the applied mathematician.
- If you cannot solve the proposed problem, try to solve first a simpler related problem.
...The first derivative, the result of the differentiation of with respect to , was written by Leibniz in the form ...Leibniz's notation ...is both extremely useful and dangerous. Today, as the concepts of limit and derivative are sufficiently clarified, the use of the notation... need not be dangerous. Yet, the situation was different in the 150 years between the discovery of calculus by Newton and Leibniz and the time of Cauchy. The derivative was considered as the ratio of two "infinitely small quanitites", of the infinitesimals and . ...it greatly facilitated the systematization of the rules of the calculus and gave intuitive meaning to its formulas. Yet this consideration was also obscure... it brought mathematics into disrepute... some of the best minds... such as... Berkeley, complained that calculus is incomprehensible. ... is the limit of a ratio of to ... Once we have realized this sufficiently clearly, we may, under certain circumstances, treat so as if it were a ratio... and multiply by to achieve the separation of variables. We get
- Simplicity is worth buying if we do not have to pay too great a loss of precision for it.
- Even if without the Scott's proverbial thrift, the difficulty of solving differential equations is an incentive to using them parsimoniously. Happily here is a commodity of which a little may be made to go a long way. ...the equation of small oscillations of a pendulum also holds for other vibrational phenomena. In investigating swinging pendulums we were, albeit unwittingly, also investigating vibrating tuning forks.
- The differential equation of the first order
...prescribes the slope at each point of the plane (or at each point of a certain region of the plane we call the field"). ...a differential equation of the first order... can be conceived intuitively as a problem about the steady flow of a river: Being given the direction of the flow at each point, find the streamlines. ...It leaves open the choice between the two possible directions in the line of a given slope. Thus... we should say specifically "direction of an unoriented straight line" and not merely "direction."
- Life is full of surprises: our approximate condition for the fall of a body through a resisting medium is precisely analogous to the exact condition for the flow of an electric current through a resisting wire [of an induction coil]. ...
This is the form most convenient for making an analogy with the "fall", i.e., flow, of an electric current.
...in order from left to right, mass , rate of change of velocity , gravitational force , and velocity . What are the electrical counterparts? ...To press the switch, to allow current to start flowing is the analogue of opening the fingers, to allow the body to start falling. The fall of the body is caused by the force due to gravity; the flow of the current is caused by the electromotive force or tension due to the battery. The falling body has to overcome the frictional resistance of the air; the flowing current has to overcome the electrical resistance of the wire. Air resistance is proportional to the body's velocity ; electrical resistance is proportional to the current . And consequently rate of change of velocity corresponds to rate of change of current . ...The electromagnetic induction opposes the change of current... And doesn't the inertia or mass ..? Isn't , so to speak, an electromagnetic inertia?
Mathematical Discovery (Volume 1)
[edit]- People tell you that wishful thinking is bad. Do not believe it, this is just one of those generally accepted errors.
- p. 6
About George Pólya
[edit]- If we could be any mathematician in the history of the world (besides ourselves), who would we rather be? ...we narrowed the choice down to Euler and Pólya, and finally settled on George Pólya because of the sheer enjoyment of mathematics that he has conveyed by so many examples.
- Donald E. Knuth, comments at Pólya's 90th birthday celebration quoted by Gerald L. Alexanderson, The Random Walks of George Polya (2000)
- For mathematics education and the world of problem solving it marked a line of demarcation between two eras, problem solving before and after Polya.
- A. H. Schoenfeld, in "Polya, Problem Solving, and Education" in Mathematics Magazine (1987)



















