Gottlob Frege
Appearance

Friedrich Ludwig Gottlob Frege (8 November 1848 – 26 July 1925) was a German mathematician, logician and philosopher considered to be one of the founders of modern logic. He made major contributions to the foundations of mathematics.
Quotes
[edit]- If the task of philosophy is to break the domination of words over the human mind [...], then my concept notation, being developed for these purposes, can be a useful instrument for philosophers [...] I believe the cause of logic has been advanced already by the invention of this concept notation.
- Begriffsschrift (1879) Preface to the Begriffsschrift
- This ideography is a "formula language", that is, a lingua characterica, a language written with special symbols, "for pure thought", that is, free from rhetorical embellishments, "modeled upon that of arithmetic", that is, constructed from specific symbols that are manipulated according to definite rules.
- paraphrasing Frege's Begriffsschrift, a formula language, modeled upon that of arithmetic, for pure thought (1879) in Jean Van Heijenoort ed., in From Frege to Gödel: A Source Book in Mathematical Logic, 1879-1931 (1967)
- I hope I may claim in the present work to have made it probable that the laws of arithmetic are analytic judgments and consequently a priori. Arithmetic thus becomes simply a development of logic, and every proposition of arithmetic a law of logic, albeit a derivative one. To apply arithmetic in the physical sciences is to bring logic to bear on observed facts; calculation becomes deduction.
- Gottlob Frege (1950 [1884]). The Foundations of Arithmetic. p. 99.
- Nur im Zusammenhange eines Satzes bedeuten die Wörter etwas. Es wird also darauf ankommen, den Sinn eines Satzes zu erklären, in dem ein Zahlwort vorkommt.
- Since it is only in the context of a proposition that words have any meaning, our problem becomes this: To define the sense of a proposition in which a number-word occurs.
- Gottlob Frege (1950 [1884]). p. 73
- Your discovery of the contradiction caused me the greatest surprise and, I would almost say, consternation, since it has shaken the basis on which I intended to build arithmetic.
- "Letter to Bertrand Russel" (1902) in J. van Heijenoort, ed., From Frege to Godel: A Source Book in Mathematical Logic, 1879-1931 (1967)
- 'Facts, facts, facts,' cries the scientist if he wants to emphasize the necessity of a firm foundation for science. What is a fact? A fact is a thought that is true. But the scientist will surely not recognize something which depends on men's varying states of mind to be the firm foundation of science.
- Gottlob Frege (1956). "The thought: A logical inquiry" in: Peter Ludlow (1997) Readings in the Philosophy of Language. p. 27
- It really is worth the trouble to invent a new symbol if we can thus remove not a few logical difficulties and ensure the rigour of the proofs. But many mathematicians seem to have so little feeling for logical purity and accuracy that they will use a word to mean three or four different things, sooner than make the frightful decision to invent a new word.
- Gottlob Frege in: Dagobert David Runes (1962). Readings in epistemology, theory of knowledge and dialectics. p. 334
- If I compare arithmetic with a tree that unfolds upward into a multitude of techniques and theorems while its root drives into the depths, then it seems to me that the impetus of the root.
- Gottlob Frege, Montgomery Furth (1964). The Basic Laws of Arithmetic: Exposition of the System. p. 10
- Every good mathematician is at least half a philosopher, and every good philosopher is at least half a mathematician.
- Attributed to Frege in: A. A. B. Aspeitia (2000), Mathematics as grammar: 'Grammar' in Wittgenstein's philosophy of mathematics during the Middle Period, Indiana University, p. 25
- Ein Philosoph, der keine Beziehung zur Geometrie hat, ist nur ein halber Philosoph, und ein Mathematiker, der keine philosophische Ader hat, ist nur ein halber Mathematiker.
- A philosopher who has no connection to geometry is only half a philosopher, and a mathematician who has no philosophical vein is only half a mathematician.
- Gottlob Frege: Erkenntnisquellen der Mathematik und der mathematischen Naturwissenschaften, 1924/1925, submitted to Wissenschaftliche Grundlagen; posthumously published in: Frege, Gottlob: Nachgelassene Schriften und Wissenschaftlicher Briefwechsel. Felix Meiner Verlag, 1990, p. 293
Über Sinn und Bedeutung, 1892
[edit]- Gottlob Frege (1892) On Sense and Reference. paper
- A judgment, for me is not the mere grasping of a thought, but the admission of its truth.
- Gottlob Frege (1892). On Sense and Reference, note 7.
- Equality gives rise to challenging questions which are not altogether easy to answer... a = a and a = b are obviously statements of differing cognitive value; a = a holds a priori and, according to Kant, is to be labeled analytic, while statements of the form a = b often contain very valuable extensions of our knowledge and cannot always be established a priori. The discovery that the rising sun is not new every morning, but always the same, was one of the most fertile astronomical discoveries. Even to-day the identification of a small planet or a comet is not always a matter of course. Now if we were to regard equality as a relation between that which the names 'a' and 'b' designate, it would seem that a = b could not differ from a = a (i.e. provided a = b is true). A relation would thereby be expressed of a thing to itself, and indeed one in which each thing stands to itself but to no other thing.
- As cited in: M. Fitting, Richard L. Mendelsoh (1999), First-Order Modal Logic, p. 142. They called this Frege's Puzzle.
- Without some affinity in human ideas art would certainly be impossible; but it can never be exactly determined how far the intentions of the poet are realized.
- Gottlob Frege (1892). On Sense and Reference.
Grundgesetze der Arithmetik, 1893 and 1903
[edit]- Gottlob Frege (vol. 1, 1893; vol. 2, 1903). Grundgesetze der Arithmetik. Translation: The Foundations of Arithmetic or The Basic Laws of Arithmetic
- Being true is different from being taken as true, whether by one or by many or everybody, and in no case is it to be reduced to it. There is no contradiction in something's being true which everybody takes to be false. I understand by 'laws of logic' not psychological laws of takings-to-be-true, but laws of truth. ...If being true is thus independent of being acknowledged by somebody or other, then the laws of truth are not psychological laws: they are boundary stones set in an eternal foundation, which our thought can overflow, but never displace. It is because of this that they have authority for our thought if it would attain truth. They do not bear the relation to thought that the laws of grammar bear to language; they do not make explicit the nature of our human thinking and change as it changes.
- Introduction, Tr. Montgomery Furth (1964)
- The ideal of strictly scientific method in mathematics which I have tried to realise here, and which perhaps might be named after Euclid I should like to describe in the following way... The novelty of this book does not lie in the content of the theorems but in the development of the proofs and the foundations on which they are based... With this book I accomplish an object which I had in view in my Begriffsschrift of 1879 and which I announced in my Grundlagen der Arithmetik. I am here trying to prove the opinion on the concept of number that I expressed in the book last mentioned.
- Vol. 1. pp. 137-140, as cited in: Ralph H. Johnson (2012), Manifest Rationality: A Pragmatic Theory of Argument, p. 87
- A scientist can hardly meet with anything more undesirable than to have the foundations give way just as the work is finished. I was put in this position by a letter from Mr. Bertrand Russell when the work was nearly through the press.
- Note in the appendix of Grundlagen der Arithmetik (Vol. 2) after Frege had received a letter of Bertrand Russell in which Russell had explained his discovery of, what is now known as, Russell's paradox.
- Is it always permissible to speak of the extension of a concept, of a class? And if not, how do we recognize the exceptional cases? Can we always infer from the extension of one concept's coinciding with that of a second, that every object which falls under the first concept also falls under the second?
- Vol. 2, p. 127. Replying to Bertrand Russell's letter about Russell's Paradox; quoted in The Stanford Encyclopedia of Philosophy
- The historical approach, with its aim of detecting how things began and arriving from these origins at a knowledge of their nature, is certainly perfectly legitimate; but it also has its limitations. If everything were in continual flux, and nothing maintained itself fixed for all time, there would no longer be any possibility of getting to know about the world, and everything would be plunged into confusion.
- Translation J. L. Austin (Oxford, 1950) as quoted by Stephen Toulmin, Human Understanding: The Collective Use and Evolution of Concepts (1972) Vol. 1, p. 55.
- We suppose, it would seem, that concepts grow in the individual mind like leaves on a tree, and we think to discover their nature by studying their growth; we seek to define them psychologically, in terms of the human mind. But this account makes everything subjective, and if we follow it through to the end, does away with truth. What is known as the history of concepts is really a history either of our knowledge of concepts or of the meanings of words.
- Translation J. L. Austin (Oxford, 1950) as quoted by Stephen Toulmin, Human Understanding: The Collective Use and Evolution of Concepts (1972) Vol. 1, p. 56.
- Often it is only after immense intellectual effort, which may have continued over centuries, that humanity at last succeeds in achieving knowledge of a concept in its pure form, by stripping off the irrelevant accretions which veil it from the eye of the mind.
- Translation J. L. Austin (Oxford, 1950) as quoted by Stephen Toulmin, Human Understanding: The Collective Use and Evolution of Concepts (1972) Vol. 1, p. 56.
Quotes about Gottlob Frege
[edit]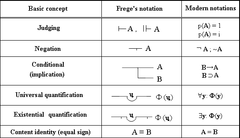
— Jeffrey A. Schiffel (2008)
- Gottlob Frege created modern logic including "for all," "there exists," and rules of proof. Leibniz and Boole had dealt only with what we now call "propositional logic" (that is, no "for all" or "there exists"). They also did not concern themselves with rules of proof, since their aim was to reach truth by pure calculation with symbols for the propositions. Frege took the opposite track: instead of trying to reduce logic to calculation, he tried to reduce mathematics to logic, including the concept of number.
- Michael J. Beeson, "The Mechanization of Mathematics," in Alan Turing: Life and Legacy of a Great Thinker (2004)
- Bertrand Russell found Frege's famous error: Frege had overlooked what is now known as the Russell paradox. Namely, Frege's rules allowed one to define the class of x such that P(x) is true for any "concept" P. Frege's idea was that such a class was an object itself, the class of objects "falling under the concept P." Russell used this principle to define the class R of concepts that do not fall under themselves. This concept leads to a contradiction... argument: (1) if R falls under itself then it does not fall under itself; (2) this contradiction shows that it does not fall under itself; (3) therefore by definition it does fall under itself after all.
- Michael J. Beeson, "The Mechanization of Mathematics," in Alan Turing: Life and Legacy of a Great Thinker (2004)
- From the medieval development of Aristotle's logic through Leibniz's Characteristica Universalis through Frege and Russell and up to the present development of symbolic logic, it could be argued that exactly the reverse [of Jacques Derrida's argument] is the case; that by emphasizing logic and rationality, philosophers have tended to emphasize written language as the more perspicuous vehicle of logical relations. Indeed, as far as the present era in philosophy is concerned, it wasn't until the 1950s that serious claims were made on behalf of the ordinary spoken vernacular languages, against the written ideal symbolic languages of mathematical logic. When Derrida makes sweeping claims about "the history of the world during an entire epoch," the effect is not so much apocalyptic as simply misinformed.
- John Searle, "Word Turned Upside Down." New York Review of Books, Volume 30, Number 16 · October 27, 1983.
- Our representative absolutist is Gottlob Frege, whose writings did as much as anything to revive the 'mathematizing' approaches of the Platonist tradition around 1900, and did so—quite explicitly—as a means of protecting philosophy from subordination to the facts of history and psychology. ...The Platonist strand in Descartes' philosophy was revived... by... Frege, who promulgated the original programme of 'conceptual analysis' in his Foundations of Arithmetic. ...Frege ...was rebelling ...against the tendency to telescope formal and prescriptive 'laws of thought', which were the proper concern of logic, with the empirical and descriptive 'laws of thinking', which were the business of cognitive psychologists... [W]e should ignore all merely empirical discoveries, whether about the development of understanding in the individual mind or about the historical evolution of our communal understanding. ...Philosophers must concern themselves with 'concepts' only as timeless, intellectual ideals, towards which the human mind struggles, at best, painfully and little by little. ...[A]ctual conceptions current in any existing community are philosophically significant only as an approximation to the eternal system of ideal 'concepts'. ...[A]ny actual, historical set of conceptions has a legitimate intellectual claim on us, only to the extent that it approximates that ideal.
- Stephen Toulmin, Human Understanding: The Collective Use and Evolution of Concepts (1972) Vol. 1, pp. 53-56.
- Logic is an old subject, and since 1879 it has been a great one.
- Willard Van Orman Quine, Methods of Logic (1950) opening statement about the effect of Frege's Begriffsschrift, published 1879.
External links
[edit]- Gottlob Frege in Stanford Encyclopedia of Philosophy
- Frege's Logic, Theorem, and Foundations for Arithmetic in Stanford Encyclopedia of Philosophy


