Hyperboloid
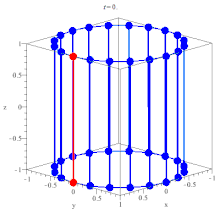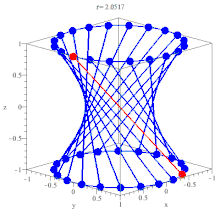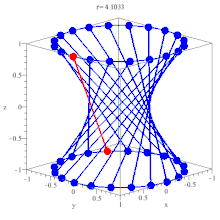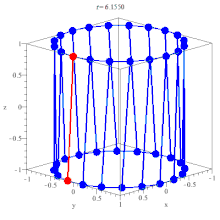

In geometry, a hyperboloid of revolution, sometimes called circular hyperboloid, is a surface that may be generated by rotating a hyperbola around one of its principal axes. An hyperboloid is a surface that may be obtained from a paraboloid of revolution by deforming it by means of directional scalings, or more generally, of an affine transformation.
A hyperboloid is a quadric surface, that is a surface that may be defined as the zero set of a polynomial of degree two in three variables. Among quadric surfaces, a hyperboloid is characterized by not being a cone or a cylinder, having a center of symmetry, and intersecting many planes into hyperbolas. A hyperboloid has also three pairwise perpendicular axes of symmetry, and three pairwise perpendicular planes of symmetry.
The hyperboloid may be described in the Cartesian coordinate system by one of the two following equations:
or
One has an hyperboloid of revolution if and only if Both of these surfaces are asymptotic to a conical surface (cone) similarly described by the equation
There are two kinds of hyperboloids. In the first case (+1 in the right-hand side of the equation), one has a one-sheet hyperboloid, also called hyperbolic hyperboloid. It is a connected surface, which has a negative Gaussian curvature at every point. This implies that the tangent plane at any point intersect the hyperboloid into two lines, and thus that the one-sheet hyperboloid is a doubly ruled surface. In the second case (−1 in the right-hand side of the equation), one has a two-sheet hyperboloid, also called elliptic hyperboloid. The surface has two connected components, and a positive Gaussian curvature at every point. Thus the surface is convex in the sense that the tangent plane at every point intersects the surface only in this point.
The hyperboloid structure, the nonimaging ideal optical concentrator, and screw theory are examples of applications of this geometric form.
 Hyperboloid of one sheet |
 Conical surface between |
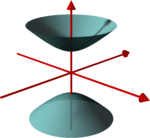 Hyperboloid of two sheets |
Quotes
[edit]- The only general ruled surface of revolution which can degenerate into a cylinder, a cone, or a plane is the hyperboloid.
- E. Asadzadeh & M. Alam, A Survey on Hyperbolic Cooling Towers (2014) World Academy of Science, Engineering and Technology, International Journal of Civil, Architectural, Structural and Construction Engineering Vol:8 No:10.
- Rotation of a hyperbola... forms a hyperboloid in which the hyperbola becomes a meridian of this surface...
- E. Asadzadeh & M. Alam, A Survey on Hyperbolic Cooling Towers (2014) World Academy of Science, Engineering and Technology, International Journal of Civil, Architectural, Structural and Construction Engineering Vol:8 No:10.
- All screws of a given pitch belonging to a system of the third order are the generators of a certain hyperboloid. There is... a different hyperboloid for each pitch. ...all these hyperboloids are concentric.
- [F]or the hyperboloid of one sheet and the hyperbolic paraboloid the curvature is negative at every point.
- Upon the hyperboloid of one sheet, and likewise upon the hyperbolic paraboloid, the two lines of striction coincide.
- Luther Pfahler Eisenhart, A Treatise on the Differential Geometry of Curves and Surfaces (1909)
- When an hyperboloid of revolution of one sheet is deformed into another ruled surface, the circle of gorge becomes a Bertrand curve and the generators are parallel to the corresponding binormals of the conjugate Bertrand curve.
- The hyperboloid of revolution (generated as a surface of revolution) is a special case of the elliptical hyperboloid... The shape of a small portion of the hyperboloid of revolution around the equator is similar to that of the catenoid, but larger portions are quite different, as are the Gauss maps. The image of the Gauss map of the whole hyperboloid of revolution omits disks around the north and south poles, whereas the image of the Gauss map of the whole catenoid omits only the north and south poles.
- Alfred Gray, Modern Differential Geometry of Curves and Surfaces with Mathematica (1999) 2nd edition, Ch. 20 Surfaces of Revolution
- One way to deal with the matters... is to work with a set of numerical values. I can do this with the help of Ball's Cartesian equation for the hyperboloids of reguli of the 3-system (1900). This equation is quoted and proved by Hunt (1978)... I shall choose the three principle screws of a 3-system of motion... I have, (a) accorded with convention, (b) ensured that the pitch quadric will be real... Ball's equation... clearly represents a series of concentric quadric surfaces... This circumstance of there being none of the concentric hyperboloids coaxial with one of the principal axes is a characteristic of the 3-system. ...within a certain, central zone of the system, the intersections among the hyperboloids are complicated and not easy to understand. Outside that zone, however... the hyperboloids appear in relation to one another... Each successive hyperboloid is wholly 'outside' its predecessor (or wholly 'inside' as the case may be), and no intersections are apparent. ...outside a certain, central zone, only one real screw can be found to pass through a generall chosen point...
- Jack Phillips, Freedom in Machinery (1984, 1990) Appendix 6C Notes on the quasi-general 3-system
- The equation of the tangent plane at the point (a, 0, 0) of the conicoid is ; this meets the surface in straight lines whose projection on the plane are given by the equation . These lines are clearly real when the surface is an hyperboloid of one sheet, and imaginary when the surface is an ellipsoid, or an hyperboloid of two sheets.
Hence the hyperboloid of one sheet is a ruled surface.
The hyperbolic paraboloid is a particular case of the hyperboloid of one sheet; hence the hyperbolic paraboloid is also a ruled surface.
This can be proved at once from the equation of the paraboloid. For, the tangent plane at the origin is , and this meets the paraboloid in the straight lines given by the equations ; the lines are clearly real when a and b have different signs, and are imaginary when a and b have the same sign.
Hence an hyperboloid of one sheet (including an hyperbolic paraboloid as a particular case) is the only ruled conicoid in addition to a cone, a cylinder, and a pair of planes.- Charles Smith, An Elementary Treatise on Solid Geometry (1884) Ch. 5 Generating Lines of Conicoids
- Suppose we start with a disk radiator and we place a mirror in the form of a hyperboloid of revolution coincident with a set of flow lines... We truncate the mirror at some distance so the open end is a circle... Considering the inside as a mirror, this forms a nonimaging concentrator with unusual properties. The foci of the hyperbolas in this section are at... the ends of the diameter of the original disk. Then all rays entering the aperture... and pointing somewhere inside the disk will be reflected by the mirror so as to strike, eventually, the inner disk... Thus, the concentrator takes all rays from the virtual source... which can pass the entry aperture... and concentrate them into an exit aperture. This result is easily proved for rays in the meridional section... the extreme angle rays emerge from the exit aperture but only after an infinite number of reflections. ...rays at angles inside the extreme angles all emerge. Thus, in the meridional plane this is a concentrator of maximal theoretical concentration. This property holds for skew rays, although this is not quite so obvious. ...When used in reverse, the same design produces a virtual ring that fills the space between a Lambertian source and the larger diameter... [disk]. The visual effect produced is striking.
- Roland Winston, Juan C. Miñano, Pablo Benítez, Nonimaging Optics (2005) Ch. 6, The Flow-line Method for Designing Nonimaging Optical Systems
- [F]or the bare hyperboloid, both real and Lambertian sources are in the same plane. This is a limitation in certain applications; however, we can manipulate these positions with lenses to place the sources at more convenient locations. ...this is an ideal concentrator. ...we have postulated an ideal lens while the hyperboloid is an ideal concentrator, albeit operating on a virtual source. The design considerations readily follow from the geometry of the hyperbola.
- Roland Winston, Juan C. Miñano, Pablo Benítez, Nonimaging Optics (2005) Ch. 6, The Flow-line Method for Designing Nonimaging Optical Systems
- A surface which may be generated by a moving straight line is called a ruled surface. The plane, the cone, and the cylinder are simple examples... the hyperbolic paraboloid is a ruled surface. ...[T]he unparted hyperboloid is a ruled surface having two sets of rectilinear generators, i.e., ...through every point of it two straight lines may be drawn, each of which shall lie entirely on the surface.
- Frederick Shenstone Woods, Frederick Harold Bailey, A Course in Mathematics for Students of Engineering and Applied Science (1909) Vol. 2 Integral Calculus, Functions of Several Variables, Space Geometry Differential Equations
- If we write the equation of the hyperboloid in the form
It is evident that (1) is the product of two equations for any value of . But (2) are the equations of a straight line... Moreover this straight line lies entirely on the surface, since the coordinates of every point of it satisfy (2) and hence (1). As different values are assigned to , we obtain a series of straight lines lying entirely on the surface.
Conversely if is any point of (1),Therefore determines the same value of from both equations (2). Hence every point of (1) lies in one and only one line (2).
We may also regard (1) as the product of the two equationswhence it is evident that there is a second set of straight lines lying entirely on the surface, one and only one of which may be drawn through any point of the surface.
Equations (2) and (3) are the equations of the rectilinear generators, and every point of the surface may be regarded as the point of intersection of one line from each set.- Frederick Shenstone Woods, Frederick Harold Bailey, A Course in Mathematics for Students of Engineering and Applied Science (1909) Vol. 2 Integral Calculus, Functions of Several Variables, Space Geometry Differential Equations
See also
[edit]External links
[edit]- Hyperboloid @Wolfram MathWorld
- YouTube Videos
- Hyperboloid of Revolution (Mar 10, 2012) Design/Constructed by Bob Lemay (LemayB1)
- Quadric Surface: The Hyperboloid of One Sheet from James Sousa, Phoenix College (Mathispower4u)
- V1 Construction of Hyperboloid of Revolution - Asymptote Method from Shane Breen



















