Judea Pearl

Judea Pearl

Judea Pearl (born 1936) is an Israeli-born American computer scientist and philosopher, best known for championing the probabilistic approach to artificial intelligence and the development of Bayesian networks. He is the 2011 winner of the ACM Turing Award, the highest distinction in computer science, "for fundamental contributions to artificial intelligence through the development of a calculus for probabilistic and causal reasoning."

Quotes

• The research questions that motivate most quantitative studies in the health, social and behavioral sciences are not statistical but causal in nature. For example, what is the efficacy of a given drug in a given population? Whether data can prove an employer guilty of hiring discrimination? What fraction of past crimes could have been avoided by a given policy? What was the cause of death of a given individual, in a specific incident? These are causal questions because they require some knowledge of the data-generating process; they cannot be computed from the data alone.
  • Pearl, Judea (2008) "Causal Inference," in: Pearl, Judea. The science and ethics of causal modeling. (2010).

• Traditional statistics is strong in devising ways of describing data and inferring distributional parameters from sample. Causal inference requires two additional ingredients: a science-friendly language for articulating causal knowledge, and a mathematical machinery for processing that knowledge, combining it with data and drawing new causal conclusions about a phenomenon.
  • Pearl, Judea. "Causal inference in statistics: An overview." Statistics Surveys 3 (2009): 96-146.

• Haavelmo was the first to recognize the capacity of economic models to guide policies. This paper describes some of the barriers that Haavelmo’s ideas have had (and still have) to overcome, and lays out a logical framework that has evolved from Haavelmo’s insight and matured into a coherent and comprehensive account of the relationships between theory, data and policy questions. The mathematical tools that emerge from this framework now enable investigators to answer complex policy and counterfactual questions using simple routines, some by mere inspection of the model’s structure.
  • Judea Pearl, "Trygve Haavelmo and the emergence of causal calculus." University of California Los Angeles, Computer Science Department, CA. 2012.

Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference, 1988

• Mr. Holmes receives a telephone call from his neighbor Dr. Watson who states that he hears the sound of a burglar alarm from the direction of of Mr. Holmes' house. While preparing to rush home, Mr. Holmes recalls that Dr. Watson is known to be a tasteless practical joker...
  • p. 42: Example of an uncertain evidence

• When loops are present, the network is no longer singly connected and local propagation schemes will invariably run into trouble.. If we ignore the existence of loops and permit the nodes to continue communicating with each other as if the network were singly connected, messages may circulate indefinitely around the loops and process may not converges to a stable equilibrium... Such oscillations do not normally occur in probabilistic networks... which tend to bring all messages to some stable equilibrium as time goes on. However, this asymptotic equilibrium is not coherent, in the sense that it does not represent the posterior probabilities of all nodes of the network.
  • p. 195

Causality: Models, Reasoning, and Inference, 2000

• Simpson's paradox (Simpson 1951; Blyth 1972), first encountered by Pearson in 1899 (Aldrich 1995), refers to the phenomenon whereby an event C increases the probability of E in a given population p and, at the same time, decreases the probability of E in every subpopulation of p.
  • p. 1

A simple Bayesian network. Rain influences whether the sprinkler is activated, and both rain and the sprinkler influence whether the grass is wet.

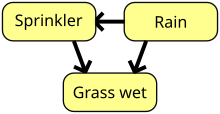
• Bayesian networks [is] a term coined in Pearl (1985) to emphasize three aspects: (1) the subjective nature of the input information; (2) the reliance on Bayes' conditioning as the basis of updating information; (3) the distinction between causal and evidential models of reasoning, a distinction that underscores Thomas Bayes' paper of 1763,
  • p. 14

• A quantity Q(M) is identifiable, given a set of assumptions A, iffor any two models M1 and M2 that satisfy A, we have

P(M1) = P(M2) ⇒ Q(M1) = Q(M2)

• • p. 77 : cited in: Rick H. Hoyle (2014). Handbook of Structural Equation Modeling. p. 75
  • Hoyle (2014) further explained: In words, the functional details of M1 and M2 do not matter; what matters is that the assumptions in A (e.g. those encoded in the diagram) would constrain the variability of those details in such a way that equality of P's would entail equality of Q's. When this happens, Q depends on P only and should therefore be expressible in terms of the parameters of P. The section “Identification Using Graphs” will exemplify and operationalize this notion.

• An event recognised as responsible for the production of a certain outcome... Human intuition is extremely keen in detecting and ascertaining this type of causation and hence is considered the key to construct explanations... and the ultimate criterion (known as “cause in fact”) for determining legal responsibility.
  Clearly, actual causation requires information beyond that of necessity and sufficiency: the actual process mediating between the cause and the effect must enter into consideration.
  • p. 309, as cited in: Rinke Hoekstra (2009), Ontology Representation: Design Patterns and Ontologies... p. 181

Quotes about Judea Pearl

• Judea Pearl's work has transformed artificial intelligence (AI) by creating a representational and computational foundation for the processing of information under uncertainty. Pearl's work went beyond both the logic-based theoretical orientation of AI and its rule-based technology for expert systems. He identified uncertainty as a core problem faced by intelligent systems and developed an algorithmic interpretation of probability theory as an effective foundation for the representation and acquisition of knowledge.
  • Stuart J. Russell. "Judea Pearl, ACM A.M. Turing Award, United States – 2011." at awards.acm.org.

See also

• Daniel Pearl