Jump to content

Theory of relativity

From Wikiquote
(Redirected from Relativity theory)
Pictorial analogy of general relativity's
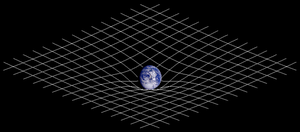
spacetime curvature.

The theory of relativity, or simply relativity in physics, usually encompasses two interrelated theories by Albert Einstein: special relativity and general relativity. Special relativity applies to elementary particles and their interactions, describing all their physical phenomena except gravity. General relativity explains the law of gravitation and its relation to other forces of nature. It applies to the cosmological and astrophysical realm, including astronomy.

The theory transformed theoretical physics and astronomy during the 20th century, superseding a 200-year-old theory of mechanics created primarily by Isaac Newton. It introduced concepts including spacetime as a unified entity of space and time, relativity of simultaneity, kinematic and gravitational time dilation, and length contraction.

Quotes

[edit]
  • [T]he program which Immanuel Kant proposed back in the 1760s... was this: our knowledge of the outside world depends on our modes of perception... Unfortunately, a great revolution took place in or about the year 1768, when he read a paper by Euler which intended to show that space was indeed absolute as Newton had suggested and not relative as Leibnitz suggested. (...in the eighteenth century the question of whether Newton's... or Leibnitz's view of the world was right profoundly affected all philosophy.) After reading Euler's argument... Kant... for the first time proposed that... we must be conscious of [absolute space] a priori. ...Kant died in 1804, long before new ideas about space... had been published... And since one of the things that happened in [our] lifetime has been the substitution of... a Leibnitz universe, the universe of relativity, for Newton's universe... we should think that out again.
  • Riemann has shewn that as there are different kinds of lines and surfaces, so there are different kinds of space of three dimensions; and that we can only find out by experience to which of these kinds the space in which we live belongs. In particular, the axioms of plane geometry are true within the limits of experiment on the surface of a sheet of paper, and yet we know that the sheet is really covered with a number of small ridges and furrows, upon which (the total curvature not being zero) these axioms are not true. Similarly, he says although the axioms of solid geometry are true within the limits of experiment for finite portions of our space, yet we have no reason to conclude that they are true for very small portions; and if any help can be got thereby for the explanation of physical phenomena, we may have reason to conclude that they are not true for very small portions of space.
    • William Kingdon Clifford, "On the Space-Theory of Matter," Abstract (read Feb 21, 1870) from the Cambridge Philosophical Society's Proceedings II (1876) pp. 157-158, see also Clifford, Mathematical Papers (1882) pp. 21-22
  • I hold in fact
    (1) That small portions of space are in fact of a nature analogous to little hills on a surface which is on the average flat; namely, that the ordinary laws of geometry are not valid in them.
    (2) That this property of being curved or distorted is continually being passed on from one portion of space to another after the manner of a wave.
    (3) That this variation of the curvature of space is what really happens in that phenomenon which we call the motion of matter, whether ponderable or etherial.
    (4) That in the physical world nothing else takes place but this variation, subject possibly to the law of continuity.
    • William Kingdon Clifford, "On the Space-Theory of Matter," Abstract (read Feb 21, 1870) from the Cambridge Philosophical Society's Proceedings II (1876) pp. 157-158
  • No mathematician can give any meaning to the language about matter, force, inertia used in current text-books of mechanics.
  • We may... be treating merely as physical variations effects which are really due to changes in the curvature of our space; whether, in fact, some or all of those causes which we term physical may not be due to the geometrical construction of our space. There are three kinds of variation in the curvature of our space which we ought to consider as within the range of possibility.
    (i) Our space is perhaps really possessed of a curvature varying from point to point, which we fail to appreciate because we are acquainted with only a small portion of space, or because we disguise its small variations under changes in our physical condition which we do not connect with our change of position. The mind that could recognise this varying curvature might be assumed to know the absolute position of a point. For such a mind the postulate of the relativity of position would cease to have a meaning. It does not seem so hard to conceive such a state of mind as the late Professor Clerk-Maxwell would have had us believe. It would be one capable of distinguishing those so-called physical changes which are really geometrical or due to a change of position in space.
    (ii) Our space may be really same (of equal curvature), but its degree of curvature may change as a whole with the time. In this way our geometry based on the sameness of space would still hold good for all parts of space, but the change of curvature might produce in space a succession of apparent physical changes.
    (iii) We may conceive our space to have everywhere a nearly uniform curvature, but that slight variations of the curvature may occur from point to point, and themselves vary with the time. These variations of the curvature with the time may produce effects which we not unnaturally attribute to physical causes independent of the geometry of our space. We might even go so far as to assign to this variation of the curvature of space 'what really happens in that phenomenon which we term the motion of matter.'
  • The modern theory of relativity, on its mathematical side, is merely an elaboration of Riemann's analysis.
  • It is the reciprocity of these appearances—that each party should think the other has contracted—that is so difficult to realise. Here is a paradox beyond even the imagination of Dean Swift. Gulliver regarded the Lilliputians as a race of dwarfs; and the Lilliputians regarded Gulliver as a giant. That is natural. If the Lilliputians had appeared dwarfs to Gulliver, and Gulliver had appeared a dwarf to the Lilliputians—but no! that is too absurd for fiction, and is an idea only to be found in the sober pages of science. ...It is not only in space but in time that these strange variations occur. If we observed the aviator carefully we should infer that he was unusually slow in his movements; and events in the conveyance moving with him would be similarly retarded—as though time had forgotten to go on. His cigar lasts twice as long as one of ours. ...But here again reciprocity comes in, because in the aviator's opinion it is we who are travelling at 161,000 miles a second past him; and when he has made all allowances, he finds that it is we who are sluggish. Our cigar lasts twice as long as his.
  • ...The present revolution of scientific thought follows in natural sequence on the great revolutions at earlier epochs in the history of science. Einstein's special theory of relativity, which explains the indeterminateness of the frame of space and time, crowns the work of Copernicus who first led us to give up our insistence on a geocentric outlook on nature; Einstein's general theory of relativity, which reveals the curvature or non-Euclidean geometry of space and time, carries forward the rudimentary thought of those earlier astronomers who first contemplated the possibility that their existence lay on something which was not flat. These earlier revolutions are still a source of perplexity in childhood, which we soon outgrow; and a time will come when Einstein's amazing revelations have likewise sunk into the commonplaces of educated thought.
  • If you don't take my words too seriously, I would say this: If we assume that all matter would disappear from the world, then, before relativity, one believed that space and time would continue existing in an empty world. But, according to the theory of relativity, if matter and its motion disappeared there would no longer be any space or time.
    • Albert Einstein (1921) as quoted by Philipp Frank, Einstein, His Life and Times (1947) 1st edition, Ch. VIII, Sect. 5, p. 178. In response to the question by an American journalist: How could one explain the content of the relativity theory in a few sentences?
  • Another topic deserving discussion is Einstein’s modification of Newton’s law of gravitation. In spite of all the excitement it created, Newton’s law of gravitation is not correct! It was modified by Einstein to take into account the theory of relativity. According to Newton, the gravitational effect is instantaneous, that is, if we were to move a mass, we would at once feel a new force because of the new position of that mass; by such means we could send signals at infinite speed. Einstein advanced arguments which suggest that we cannot send signals faster than the speed of light, so the law of gravitation must be wrong. By correcting it to take the delays into account, we have a new law, called Einstein’s law of gravitation. One feature of this new law which is quite easy to understand is this: In the Einstein relativity theory, anything which has energy has mass—mass in the sense that it is attracted gravitationally. Even light, which has an energy, has a “mass.” When a light beam, which has energy in it, comes past the sun there is an attraction on it by the sun. Thus the light does not go straight, but is deflected. During the eclipse of the sun, for example, the stars which are around the sun should appear displaced from where they would be if the sun were not there, and this has been observed.

  • For over 200 years the equations of motion enunciated by Newton were believed to describe nature correctly, and the first time that an error in these laws was discovered, the way to correct it was also discovered. Both the error and its correction were discovered by Einstein in 1905.

    Newton’s Second Law, which we have expressed by the equation : was stated with the tacit assumption that m is a constant, but we now know that this is not true, and that the mass of a body increases with velocity. In Einstein’s corrected formula m has the value : where the “rest mass” m0 represents the mass of a body that is not moving and c is the speed of light, which is about 3×105 km⋅sec−1 or about 186,000 mi⋅sec−1.

  • One clock stayed on the ground; its double flew. / And it ran slow. So, then. The mad thing's true.
  • The modern world began on 29 May 1919 when photographs of a solar eclipse, taken on the island of Principe off West Africa and at Sobral in Brazil, confirmed the truth about a new theory of the universe. It had been apparent for half a century that the Newtonian cosmology, based upon the straight lines of Euclidean geometry, and Galileo's notions of absolute time, was in need of serious modification. It had stood for more than two hundred years. It was the framework within which the European Enlightenment, the Industrial Revolution, the vast expansion of human knowledge, freedom, and prosperity which had characterized the nineteenth century, had taken place. But increasingly powerful telescopes were revealing anomalies. In particular, the motions of the planet Mercury deviated by forty-three seconds of an arc a century from its predictable behavior under Newtonian laws of physics. Why? In 1905, a twenty-six-year old German Jew, Albert Einstein, then working in the Swiss patent office in Berne, had published a paper, 'On the electrodynamics of moving bodies,' which became known as the Special Theory of Relativity. Einstein's observations on the way in which, in certain circumstances, lengths appeared to contract and clocks to slow down, are analogous to the effects of perspective in painting. In fact the discovery that space and time are relative rather than absolute terms of measurement is comparable, in its effect on our perception of the world, to the first use of perspective in art, which occurred in Greece in the two decades c.500-480 BC.
  • The originality of Einstein, amounting to a form of genius, and the curious elegance of his lines of argument, which colleagues compared to a kind of art, aroused growing, world-wide interest. In 1907 he published a demonstration that all mass was energy, encapsulated in the equation E = mc2, which a latter age saw as the starting point in the race for the A-bomb. Not even the onset of the European war prevented scientists from following his quest for an all-embracing General Theory of Relativity which would cover gravitational fields and provide a comprehensive revision of Newtonian physics. In 1915 news reached London that he had done it. The following spring, as the British were preparing their vast and catastrophic offensive on the Somme, the key paper was smuggled through the Netherlands and reached Cambridge, where it was received by Arthur Eddington, Professor of Astronomy and Secretary of the Royal Astronomical Society
  • What makes writing relativity so tricky is this: Built into ordinary language — in its use of tenses, for example — are many implicit assumptions about the nature of temporal relations that we now know to be false. Most importantly, we have known since 1905 that when you say that two events in different places happen at the same time you are not referring to anything inherent in the events themselves. You are merely adopting a conventional way of locating them that can differ from other equally valid conventional assignments of temporal order which do not have the events happening at the same time.
  • It was the space doctor who figured out the answer. He said that if our ideas about light were right, then our ideas about distance and seconds must be wrong. He said that time doesn’t pass the same for everyone. When you go fast, he said, the world around you changes shape, and time outside starts moving slower.
    The doctor came up with some numbers for how time and space must change to make the numbers for light work. With his idea, everyone would see light moving the right distance every second. This idea is what we call his special idea.
    The special idea is really, really strange, and understanding it can take a lot of work. Lots of people thought it must be wrong because it’s so strange, but it turned out to be right. We know because we’ve tried it out. If you go really fast, time goes slower. If you’re in a car, you see watches outside the car go slower. They only go a little slower, so you wouldn’t notice it in your normal life; it takes the best watches in the world to even tell that it’s happening. But it really does happen.
  • After the doctor figured out the special idea, he started thinking about weight. Things with weight pull on each other. Earth pulls things down toward it, which is why you can’t jump to space. Earth also pulls on the moon, keeping it near us, and the sun pulls on Earth in the same way. It turns out that light gets pulled by weight, too. (People weren’t sure about this for a while, because it moves so fast that it only gets pulled a little.)
    Someone very careful might notice that this gives us a new problem: How can light turn? The numbers that explain how light moves also say that it can only go forward. It can’t change direction in empty space. That’s just what the numbers for light say—the same numbers that say it always moves a certain distance every second.
    If a light wave is pulled down, it has to turn to point down, since it can’t travel to the side. To turn, the bottom part of the wave has to go slower than the top part, since it’s going a shorter distance in the same time. But that can’t be right, because the numbers say that light can’t go faster or slower. We’re in trouble again. And, once again, the space doctor has an answer.
    The space doctor figured out that to explain how weight pulls things like light, we have to play around with time again. He showed that if time itself goes slower near heavy things, then the side of the light near the heavy thing won’t go as far every second. This lets the light turn toward the heavy thing.
    The doctor’s idea was that weight slows down time, and it explained how light could bend. But to figure out how much light bends, we need to look at the other part of the doctor’s big idea. To talk about that part, let’s forget about light and instead visit another world.
  • There is a point of view according to which relativity theory is the end-point of "classical physics", which means physics in the style of Newton-Faraday-Maxwell, governed by the "deterministic" form of causality in space and time, while afterwards the new quantum-mechanical style of the laws of Nature came into play. This point of view seems to me only partly true, and does not sufficiently do justice to the great influence of Einstein, the creator of the theory of relativity, on the general way of thinking of the physicists of today. By its epistemological analysis of the consequences of the finiteness of the velocity of light (and with it, of all signal-velocities), the theory of special relativity was the first step away from naive visualization. The concept of the state of motion ,of the "luminiferous aether", as the hypothetical medium was called earlier, had to be given up, not only because it turned out to be unobservable, but because it became superfluous as an element of a mathematical formalism, the group-theoretical properties of which would only be disturbed by it.
  • By the widening of the transformation group in general relativity the idea of distinguished inertial coordinate systems could also be eliminated by Einstein as inconsistent with the group-theoretical properties of the theory. Without this general critical attitude, which abandoned naive visualizations in favour of a conceptual analysis of the correspondence between observational data and the mathematical quantities in a theoretical formalism, the establishment of the modern form of quantum theory would not have been possible.
  • I consider the theory of relativity to be an example showing how a fundamental scientific discovery, sometimes even against the resistance of its creator, gives birth to further fruitful developments, following its own autonomous course.
    • Wolfgang Pauli (1956), Preface of Theory of Relativity
  • Einstein's famous theory of relativity states that while phenomena appear different to someone close to a black hole, traveling close to the speed of light, or in a falling elevator here on earth, scientists in profoundly different environments will nevertheless always discover the same underlying laws of nature.
  • Relativity distorted classical expectations in a way that Clavain still did not find entirely intuitive. Slam two objects towards each other, each with individual velocities just below light-speed, and the classical result for their closing velocity would be the sum of their individual speeds: just under twice the speed of light. Yet the true result, confirmed with numbing precision, was that the objects saw each other approach with a combined speed that was still just below the speed of light. Similarly, the relativistic closing velocity for two objects moving towards each other with individual speeds of one-half of light-speed was not light-speed itself, but eight-tenths of it. It was the way the universe was put together, and yet it was not something the human mind had evolved to accept.
  • There is another side to the theory of relativity. ...the development of science is in the direction to make it less subjective, to separate more and more in the observed facts that which belongs to the reality behind the phenomena, the absolute, from the subjective element, which is introduced by the observer, the relative. Einstein's theory is a great step in that direction. We can say that the theory of relativity is intended to remove entirely the relative and exhibit the pure absolute.
    • Willem de Sitter, "Relativity and Modern Theories of the Universe," Kosmos (1932)
  • This is the mathematical formulation of the theory of relativity. The metric properties of the four-dimensional continuum are described... by a certain number (ten, in fact) of quantities denoted by gαβ, and commonly called "potentials." The physical status of matter and energy, on the other hand, is described by ten other quantities, denoted by Tαβ, the set of which is called the "material tensor." This special tensor has been selected because it has the property which is mathematically expressed by saying that its divergence vanishes, which means that it represents something permanent. The fundamental fact of mechanics is the law of inertia, which can be expressed in its most simple form by saying that it requires the fundamental laws of nature to be differential equations of the second order. Thus the problem was to find a differential equation of the second order giving a relation between the metric tensor gαβ and the material tensor Tαβ. This is a purely mathematical problem, which can be solved without any reference to the physical meaning of the symbols. The simplest possible equation (or rather set of ten equations, because there are ten g's) of that kind that can be found was adopted by Einstein as the fundamental equation of his theory. It defines the space-time continuum, or the "field." The world-lines of material particles and light quanta are the geodesics in the four-dimensional continuum defined by the solutions gαβ of these field-equations. The equations of the geodesic thus are equivalent to the equations of motion of mechanics. When we come to solve the field-equations and substitute the solutions in the equations of motion, we find that in the first approximation, i.e. for small material velocities (small as compared with the velocity of light), these equations of motion are the same as those resulting from Newton's theory of gravitation. The distinction between gravitation and inertia has disappeared; the gravitational action between two bodies follows from the same equations, and is the same thing, as the inertia of one body. A body, when not subjected to an extraneous force (i.e. a force other than gravitation), describes a geodesic in the continuum, just as it described a geodesic, or straight line, in the absolute space of Newton under the influence of inertia alone.
    The field-equations and the equations of the geodesic together contain the whole science of mechanics, including gravitation.
    • Willem de Sitter, "Relativity and Modern Theories of the Universe," Kosmos (1932)
  • Two points should be specially emphasized in connection with the general theory of relativity.
    First, it is a purely physical theory, invented to explain empirical physical facts, especially the identity of gravitational and inertial mass, and to coordinate and harmonize different chapters of physical theory, especially mechanics and electromagnetic theory. It has nothing metaphysical about it. Its importance from a metaphysical or philosophical point of view is that it aids us to distinguish in the observed phenomena what is absolute, or due to the reality behind the phenomena, from what is relative, i.e. due to the observer.
    Second, it is a pure generalization, or abstraction, like Newton's system of mechanics and law of gravitation. It contains no hypothesis, as contrasted with the atomic theory or the theory of quanta, which are based on hypothesis. It may be considered as the logical sequence and completion of Newton's Principia. The science of mechanics was founded by Archimedes, who had a clear conception of the relativity of motion, and may be called the first relativist. Galileo, who was inspired by the reading of the works of Archimedes, took the subject up where his great predecessor had left it. His fundamental discovery is the law of inertia, which is the backbone of Newton's classical system of mechanics, and retains the same central position in Einstein's relativistic system. Thus one continuous line of thought can be traced through the development of our insight into the mechanical processes of nature... characterized by the sequence... Archimedes, Galileo, Newton, Einstein.
  • The best presentation of the general theory [of relativity] is still Eddington's book of 1923, The Mathematical Theory of Relativity. For the planetary motion and the motion of the moon, see: de Sitter, "On Einstein's theory of gravitation and and its astronomical consequences," Monthly Notices, R. Astr. Soc. London, 76:699; 77:155. The mathematical foundation, the calculus of tensors, is given very completely in Eddington's book. For an exhaustive treatment see: Levi-Cevita, The Absolute Differential Calculus, translated by Dr. E. Perisco (1927).
    • Willem de Sitter, The Astronomical Aspect of the Theory of Relativity (1933) footnote
  • It did not last: the Devil howling 'Ho!
    Let Einstein be!' restored the status quo.
    • J. C. Squire, in "In continuation of Pope on Newton" (1926); Squire is here extending upon the famous statement of Alexander Pope:
Nature and Nature's laws lay hid in night:
God said, Let Newton be! — and all was light.
  • As quoted in The Epigrammatists : A Selection from the Epigrammatic Literature of Ancient, Mediæval, and Modern Times (1875) by Henry Philip Dodd, p. 329
  • Einstein's theory of relativity has advanced our ideas of the structure of the cosmos a step further. It is as if a wall which separated us from Truth has collapsed. Wider expanses and greater depths are now exposed to the searching eye of knowledge, regions of which we had not even a presentiment. It has brought us much nearer to grasping the plan that underlies all physical happening.

The Evolution of Scientific Thought from Newton to Einstein (1927)

[edit]
A. D'Abro, book at archive.org
  • With the new views advocated by Riemann... the texture, structure or geometry of space is defined by the metrical field, itself produced by the distribution of matter. Any non-homogeneous distribution of matter would then entail a variable structure of geometry for space from place to place. ...
    Riemann's exceedingly speculative ideas on the subject of the metrical field were practically ignored in his day, save by the English mathematician Clifford, who translated Riemann's works, prefacing them to his own discovery of the non-Euclidean Clifford space. Clifford realised the potential importance of the new ideas and suggested that matter itself might be accounted for in terms of these local variations of the non-Euclidean space, thus inverting in a certain sense Riemann's ideas. But in Clifford's day this belief was mathematically untenable. Furthermore, the physical exploration of space seemed to yield unvarying Euclideanism. ...it was reserved for the theoretical investigator Einstein, by a stupendous effort of rational thought, based on a few flimsy empirical clues, to unravel the mystery and to lead Riemann's ideas to victory. (In all fairness to Einstein... he does not appear to have been influenced directly by Riemann.) Nor were Clifford's hopes disappointed, for the varying non-Euclideanism of the continuum was to reveal the mysterious secret of gravitation, and perhaps also of matter, motion, and electricity. ...
    Einstein had been led to recognize that space of itself was not fundamental. The fundamental continuum whose non-Euclideanism was fundamental was... one of Space-Time... possessing a four-dimensional metrical field governed by the matter distribution. Einstein accordingly applied Riemann's ideas to space-time instead of to space... He discovered that the moment we substitute space-time for space (and not otherwise), and assume that free bodies and rays of light follow geodesics no longer in space but in space-time, the long-sought-for local variations in geometry become apparent. They are all around us, in our immediate vicinity... We had called their effects gravitational effects... never suspecting that they were the result of those very local variations in the geometry for which our search had been in vain....the theory of relativity is the theory of the space-time metrical field.
  • Einstein's definition... does not differ in spirit from the definitions in classical science; its sole advantage is that it entails a minimum of assumptions, and is susceptible of being realised in a concrete way permitting a high degree of accuracy in our measurements. Einstein's definition, is then, as follows: If we consider a ray of light passing through a Galilean frame, its velocity in the frame will be the same regardless of the relative motion of the luminous source and frame, and regardless of the direction of the ray. ...when it was found that contrary to the anticipations of classical science not the slightest trace of anisotropy could be detected even by ultra-precise experiment, the objections which classical science may might have presented... lost all force. ...ether drift appeared to exert no influence one way or the other. ...
    Isotropy signifies that the velocity of light is the same in all directions. And how can we ascertain the equality of a velocity in all directions when we do not yet know how to measure time? Experimenters solved the difficulty by appealing to the observation of coincidences. ...
    Waves of light leaving the centre of a sphere simultaneously are found to return to the centre also in concidence, after having suffered a reflection against a highly polished inner surface of the sphere. ...the light waves have thus covered equal distances in the same time; whence we conclude that their speed is the same in all directions.
    Inasmuch as this experiment has been performed, yielding the results we have just described, even though the ether drift caused by the earth's motion should have varied in direction and intensity, the isotropy of space to luminous propogations was thus established. (The experiment described constitutes but a schematic form of Michelson's.) It is to be noted that in this experiment the observation of coincidences is alone appealed to (even spatial measurements can be eliminated). This is because in Michelson's experiment it is not necessary to consider a sphere. The two arms of the apparatus may be of different lengths; and all that is observed is the continued coincidence of the interference-bands with markings on the instrument. When it is realised that coincidences constitute the most exact form of observation, we understand why it is that Einstein's definition is justified
  • The most precise experiments have proved the correctness of the Einsteinian laws of mechanics and...Bucherer's experiment proving the increase in mass of an electron in rapid motion is a case in point.
    Very important differences distinguish the theory of Einstein from that of Lorentz. Lorentz also had deduced from his theory that the mass of the electron should increase and grow infinite when its speed neared that of light; but the speed in question was the speed of the electron through the stagnant ether; whereas in Einstein's theory it is merely the speed with respect to the observer. According to Lorentz, the increase in mass of the moving electron was due to its deformation or Fitzgerald contraction. The contraction modified the lay of the electromagnetic field round the electron; and it was from this modification that the increase in mass observed by Bucherer was assumed to arise. In Einstein's theory, however, the increase in mass is absolutely general and need not be ascribed to the electromagnetic field of the electron in motion. An ordinary unelectrified lump of matter like a grain of sand would have increased in mass in exactly the same proportion; and no knowledge of the microscopic constitution of matter is necessary in order to predict these effects, which result directly from the space and time transformations themselves.
    Furthermore, the fact that this increase in mass of matter in motion is now due to relative motion and not to motion through the stagnant ether, as in Lorentz's theory, changes the entire outlook considerably. According to Lorentz, the electron really increased in mass, since its motion through the ether remained a reality. According to Einstein, the electron increases in mass only in so far as it is in relative motion with respect to the observer. Were the observer to be attached to the flying electron no increase in mass would exist; it would be the electron left behind which would now appear to have suffered the increase. Thus mass follows distance, duration and electromagnetic field in being a relative and having no definite magnitude of itself and being essentially dependent on the conditions of observation.
    Owing to the general validity of the Lorentz-Einstein transformations, it becomes permissible to apply them to all manner of phenomena.. ...temperature, pressure and many other physical magnitudes turned out to be relatives. ...entropy, electric charge and the velocity of light in vacuo were absolutes transcending the observer's motion. ...a number of other entities are found to be absolutes, the most important of which is that abstract mathematical quantity called the Einsteinian interval, which plays so important a part in the fabric of the new objective world of science, the world of four-dimensional space-time.
  • Consider two observers, one... moving uniformly along a straight line, the other [stationary] on the embankment. At the precise instant these two observers pass each other at a point P, a flash of light is produced at the point P. The light wave produced by the instantaneous flash will present the shape of an expanding sphere. Since the invariant velocity of light holds equally for either observer, we must assume that either observer will find himself at all times situated at the centre of the expanding sphere.
    Our first reaction might be to say: "What nonsense! How can different people, travelling apart, all be at the centre of the same sphere?" Our objection, however, would be unjustified.
  • If our world-line and that of the body which is being observed are parallel, the body is said to be at rest. But if the two world-lines are not parallel, then, when interpreting things in terms of space and time, the body will be said to be in relative motion.

See also

[edit]
[edit]
Wikipedia
Wikipedia
Wikipedia has an article about:
Retrieved from "https://en.wikiquote.org/w/index.php?title=Theory_of_relativity&oldid=3325963"